카이제곱 분석
| 예상 빈도 | 카이제곱 통계 |
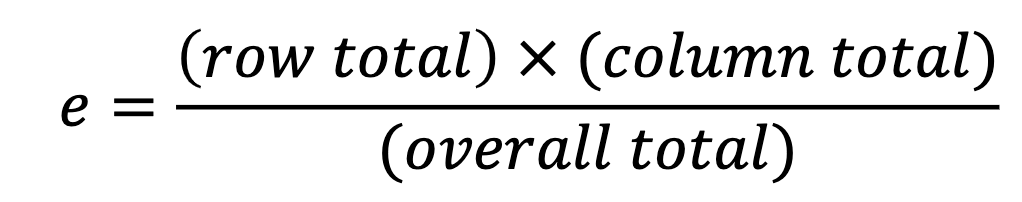
– 양방향 테이블의 셀에서 예상되는 숫자입니다. 두 개의 범주형 변수가 가정됩니다. |
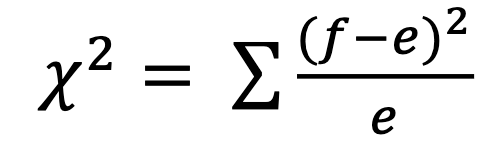
– f = 관측 빈도 / e = 예상 빈도 |
EX4) “Gender”에서 “Other” 셀과 “Readings”에서 “Sometimes” 셀의 예상 빈도를 계산합니다. 예상 빈도에 대한 해석을 제공합니다.
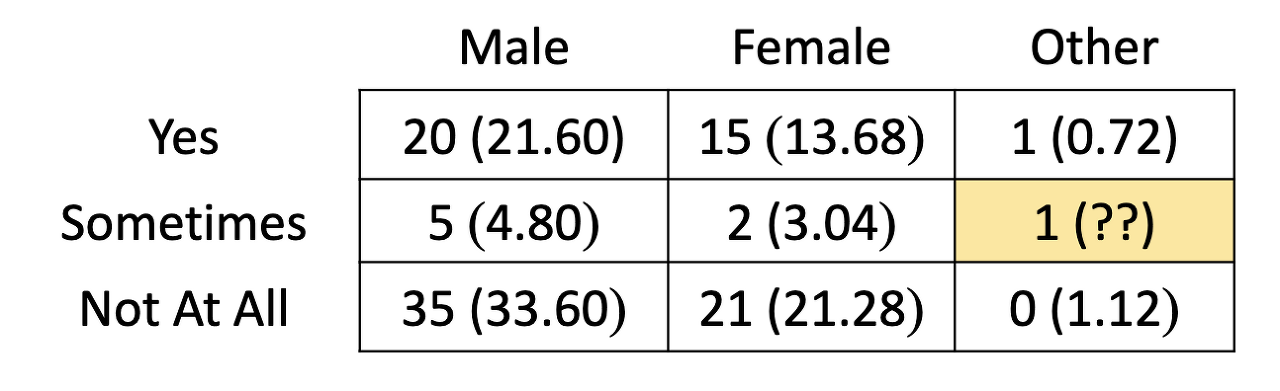
테이블
( 8 * 2 ) / 100 = 0.16
해석: 우리는 성별과 라벨 읽기가 독립적이라고 가정할 때 성별이 반대이고 때로는 라벨을 읽는 쇼핑객이 0.16명일 것으로 예상합니다.
인구에 대한 결론을 도출
| 1 단계 |

|
| 2 단계 |

r : 행 수 / c = 열 수 |
| 3단계 |

|
EX6) 다른 연구자가 유사한 연구를 수행함 더 큰 샘플로. 그는 무작위로 500명의 쇼핑객을 선택하고 성별과 포장 식품의 라벨을 정기적으로 읽는지 여부를 물었습니다. 수집된 데이터는 다음 양방향 표로 구성되었습니다.
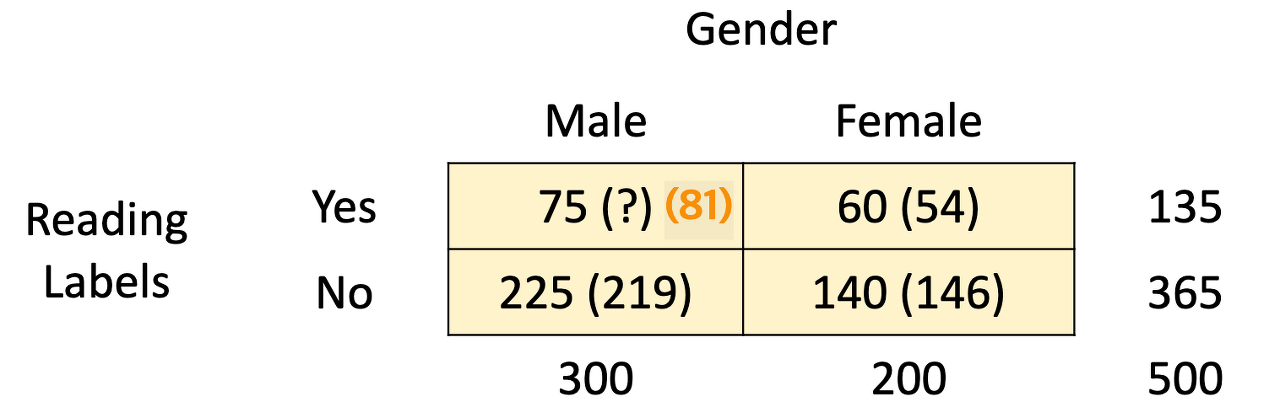
- 남성과 여성 사이에 차이가 있다는 충분한 증거가 있습니까? 포장된 식품 라벨을 읽는 습관을 가진 여성 쇼핑객?
- 당신의 것을 입력하십시오 평신도 용어로 결론.
1 단계:
Ho: 성별과 독서 라벨은 모든 쇼핑객에게 독립 변수 -> 상관관계 없음
하: 성별과 리딩 태그는 모든 쇼핑객에게 독립 변수가 아니다 -> 관계
2 단계 :
df : (2 – 1) * (2 – 1) = 1
DP : 3,841
x^2 : 4/9 + 2/3 + 12/73 + 18/73 = 1.52
3단계:
1.52(x^2) < 3.841(DP)
x^2가 DP보다 작거나 같으므로 거부할 수 없습니다. 호
우리는 성별과 독자 태그가 모든 쇼핑객에 걸쳐 상당히 독립적인 변수라는 결론을 내립니다.
-> 연결되지 않음
아마추어 표현: 남성과 여성 쇼핑객은 라벨 읽기 행동에 차이가 없습니다.
카이제곱 분석
- e >= 5 : 정확히
- e가 5보다 작다면? ⓐ 더 큰 샘플 가져오기 / ⓑ 행 또는 열을 결합하여 더 작은 양방향 표 만들기

양방향 테이블 결합
독립의 중요성을 깨닫다
- 2 변수 = 독립 -> 관계 없음 -> 다르지 않음
- 2 변수 = 종속 -> 관계 -> 다름
평신도
- Var(1-a)와 Var(1-b)는 Var(b)에서 차이가 없습니다(독립).
- Var(1-a) 및 Var(1-b)는 Var(b)에서 다릅니다(의존적).
